二十四节气在中国古代历法中扮演着非常重要的角色,本文将介绍二十四节气的基本知识,以及如何使用VSOP82/87行星运行理论计算二十四节气发生的准确时间。
中国古代历法都是以月亮运行规律为主,严格按照朔望月长度定义月,但是由于朔望月长度和地球回归年长度无法协调,会导致农历季节和天气的实际冷暖无法对应,因此聪明的古人将月亮运行规律和太阳运行规律相结合制定了中国农历的历法规则。在这种特殊的阴阳结合的历法规则中,二十四节气就扮演着非常重要的作用,它是联系月亮运行规律和太阳运行规律的纽带。正是由于二十四节气结合置闰规则,使得农历的春夏秋冬四季和地球绕太阳运动引起的天气冷暖变化相一致,成为中国几千年来生产、生活的依据。
二十四节气起源于中国黄河流域。远在春秋时代,古人就开始使用仲春、仲夏、仲秋和仲冬四个节气指导农耕种植。后来经过不断地改进与完善,到秦汉年间,二十四节气已经基本确立。公元前 104年,汉武帝颁布由邓平等人制定的《太初历》,正式把二十四节气订于历法,明确了二十四节气的天文位置。二十四节气天文位置的定义,就是从太阳黄经零度开始,沿黄经每运行15度所经历的时日称为“一个节气”。太阳一个回归年运行360度,共经历24个节气,每个公历月对应2个节气。其中,每月第一个节气为“节令”,即:立春、惊蛰、清明、立夏、芒种、小暑、立秋、白露、寒露、立冬、大雪和小寒等12个节令;每月的第二个节气为“中气”,即:雨水、春分、谷雨、小满、夏至、大暑、处暑、秋分、霜降、小雪、冬至和大寒等12个中气。“节令”和“中气”交替出现,各历时15天,人们习惯上把“节令”和“中气”统称为“节气”。
为了更好地理解二十四节气的天文位置,首先要解释几个天文学概念。“天球”是人们为了研究天体的位置和运动规律而引入的一个假象的球体,根据观察点(也就是球心)的位置不同,可分为“日心天球”、“地心天球”等等。图(1)就是天球概念的一个简单示意图:
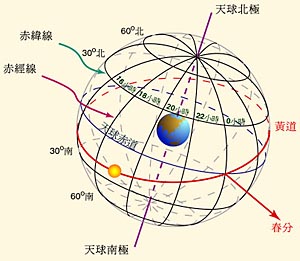
图(1)天球概念示意图
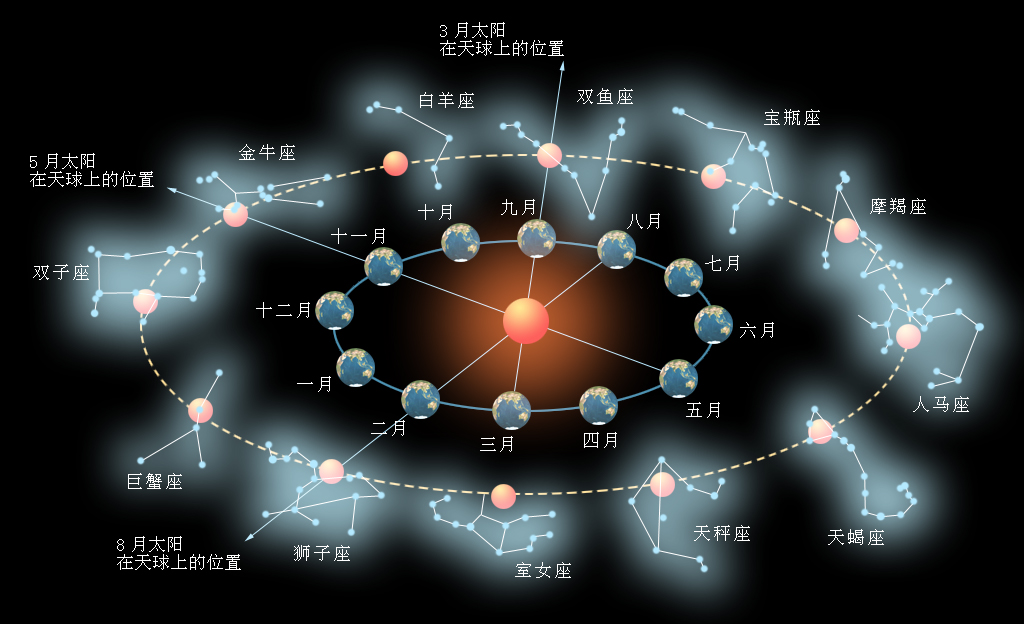
图(2)太阳黄道视觉位置原理图
double CalcSunEclipticLongitudeEC(double dt) { double L0 = CalcPeriodicTerm(Earth_L0, sizeof(Earth_L0) / sizeof(VSOP87_COEFFICIENT), dt); double L1 = CalcPeriodicTerm(Earth_L1, sizeof(Earth_L1) / sizeof(VSOP87_COEFFICIENT), dt); double L2 = CalcPeriodicTerm(Earth_L2, sizeof(Earth_L2) / sizeof(VSOP87_COEFFICIENT), dt); double L3 = CalcPeriodicTerm(Earth_L3, sizeof(Earth_L3) / sizeof(VSOP87_COEFFICIENT), dt); double L4 = CalcPeriodicTerm(Earth_L4, sizeof(Earth_L4) / sizeof(VSOP87_COEFFICIENT), dt); double L5 = CalcPeriodicTerm(Earth_L5, sizeof(Earth_L5) / sizeof(VSOP87_COEFFICIENT), dt); double L = (((((L5 * dt + L4) * dt + L3) * dt + L2) * dt + L1) * dt + L0) / 100000000.0; // 地心黄经 = 日心黄经 + 180度 return Mod360Degree(Mod360Degree(L / RADIAN_PER_ANGLE) + 180.0);}double CalcPeriodicTerm(const VSOP87_COEFFICIENT *coff, int count, double dt) { double val = 0.0; for (int i = 0; i < count; i++) { val += coff[i].A * cos(coff[i].B + coff[i].C * dt); } return val;}同样的方法计算太阳的地心黄纬:
double CalcSunEclipticLatitudeEC(double dt) { double B0 = CalcPeriodicTerm(Earth_B0, sizeof(Earth_B0) / sizeof(VSOP87_COEFFICIENT), dt); double B1 = CalcPeriodicTerm(Earth_B1, sizeof(Earth_B1) / sizeof(VSOP87_COEFFICIENT), dt); double B2 = CalcPeriodicTerm(Earth_B2, sizeof(Earth_B2) / sizeof(VSOP87_COEFFICIENT), dt); double B3 = CalcPeriodicTerm(Earth_B3, sizeof(Earth_B3) / sizeof(VSOP87_COEFFICIENT), dt); double B4 = CalcPeriodicTerm(Earth_B4, sizeof(Earth_B4) / sizeof(VSOP87_COEFFICIENT), dt); double B = (((((B4 * dt) + B3) * dt + B2) * dt + B1) * dt + B0) / 100000000.0; // 地心黄纬 = -日心黄纬 return -(B / RADIAN_PER_ANGLE);}AdjustSunEclipticLongitudeEC()函数根据3.8式计算黄经的修正量,longitude和latitude参数是由VSOP87理论计算出的太阳地心黄经和地心黄纬,单位是度,dt是儒略千年数,返回值单位是度:
double AdjustSunEclipticLongitudeEC(double dt, double longitude, double latitude) { double T = dt * 10; // T 是儒略世纪数 // 计算校正后的经度 double dbLdash = longitude - 1.397 * T - 0.00031 * T * T; // 转换为弧度 dbLdash *= RADIAN_PER_ANGLE; // 计算并返回调整值 return (-0.09033 + 0.03916 * (cos(dbLdash) + sin(dbLdash)) * tan(latitude * RADIAN_PER_ANGLE)) / 3600.0;}经过上述计算转换得到坐标值是理论值,或者说是天体的几何位置,但是FK5系统是一个目视系统,也就是说体现的是人眼睛观察效果(光学位置),这就需要根据地球的物理环境、大气环境等信息做进一步的修正,使其和人类从地球上观察星体的观测结果一致。
小知识1:天文单位
天文单位(英文:Astronomical Unit,简写AU)是一个长度的单位,约等于地球跟太阳的平均距离。天文单位是天文常数之一,是天文学中测量距离,特别是测量太阳系内天体之间的距离的基本单位。地球到太阳的平均距离大约为一个天文单位,约等于1.496亿千米。1976年,国际天文学联会把一天文单位定义为一颗质量可忽略、公转轨道不受干扰而且公转周期为365.2568983日(即一高斯年)的粒子与一个质量相等约一个太阳的物体的距离。当前普遍被接受并使用的天文单位的值是149,597,870,691±30米(约一亿五千万公里)。
小知识2:FK5系统
FK5常用的目视星表系统,又称第五基本星表,是在FK4(第四基本星表)的基础上发展出来的,对FK4星表进行了修正,于1984年正式启用。它定义了一个以太阳质心为中心,J2000.0平赤道和春分点为基准的天球平赤道坐标系。近年来国际上又编制了FK6星表(第六基本星表),但是还没有被正式启用。
【用天文方法计算二十四节气 下篇】
本篇介绍修正理论和修正算法
经过上述计算转换得到坐标值是理论值,或者说是天体的几何位置,但是FK5系统是一个目视系统,也就是说体现的是人眼睛观察效果(光学位置),这就需要根据地球的物理环境、大气环境等信息做进一步的修正,使其和人类从地球上观察星体的观测结果一致。
首先需要进行章动修正。章动是指地球沿自转轴的指向绕黄道极缓慢旋转过程中,由于地球上物质分布不均匀性和月球及其它行星的摄动力造成的轻微抖动。英国天文学家詹姆斯·布拉德利(1693—1762)最早发现了章动,章动可以沿着黄道分解为水平分量和垂直分量,黄道上的水平分量记为Δψ,称为黄经章动,它影响了天球上所有天体的经度。黄道上的垂直分量记为Δε,称为交角章动,它影响了黄赤交角。目前编制天文年历所依据的章动理论是伍拉德在1953年建立的,它是以刚体地球模型为基础的。1977年,国际天文联合会的一个专家小组建议采用非刚体地球模型――莫洛坚斯基II模型代替刚体地球模型计算章动,1979年的国际天文学联合会第十七届大会正式通过了这一建议,并决定于1984年正式实施。
地球章动主要是月球运动引起的,也具有一定的周期性,可以描述为一些周期项的和,主要项的周期是6798.4日(18.6年),但其它项是一些短周期项(小于10天)。本文采用的计算方法取自国际天文联合会的IAU1980章动理论,周期项系数数据来源于《天文算法》一书第21章的表21-A,该表忽略了IAU1980章动理论中系数小于0.0003’的周期项,因此只有63项。每个周期项包括计算黄经章动(Δψ)的正弦系数(相位内项系数)、计算交角章动的(Δε)余弦系数(相位外项系数)以及计算辐角的5个基本角距(M、M’、D、F、Ω)的线性组合系数。5个基本角距的计算公式是:
平距角(日月对地心的角距离):
D = 297.85036 455267.111480 * T – 0.0019142 * T2 T3 / 189474 (3.10式)
太阳(地球)平近点角:
M = 357.52772 35999.050340 * T – 0.0001603 * T2 – T3 / 300000 (3.11式)
月球平近点角:
M’= 134.96298 477198.867398 * T 0.0086972 * T2 T3 / 56250 (3.12式)
月球纬度参数:
F = 93.27191 483202.017538 * T – 0.0036825 * T2 T3 / 327270 (3.13式)
黄道与月球平轨道升交点黄经:
Ω= 125.04452 – 1934.136261 * T 0.0020708 * T2 T3 / 450000 (3.14式)
以上各式中的T是儒略世纪数,计算出来的5个基本角距的单位都是度,在计算正弦或余弦时要转换为弧度单位。计算每一个周期项的黄经章动过程是这样的,首先将3.10-3.14式计算出来的值与对应的5个基本角距系数组合,计算出辐角。以本文使用的章动周期项系数表中的第七项为例,5个基本角距对应的系数分别是1、0、-2、2和2,辐角θ的值就是:-2D M 2F 2Ω。计算出辐角后就可以计算周期项的值:
S = (S1 S2 * T) * sin(θ) (3.15式)
仍以第七项为例,S的值就是(-517 1.2 * T)* sin(θ)。对每一项的值S累加就可得到黄经章动,单位是0.0001’。交角章动的计算方法与黄经章动的计算类似,辐角θ的值是一样的,只是计算章动使用的是余弦系数:
C = (C1 C2 * T) * cos(θ) (3.16式)
CalcEarthLongitudeNutation()函数就是计算黄经章动的实现代码:
double CalcEarthLongitudeNutation(double dt) { double T = dt * 10; // 儒略世纪数 double D, M, Mp, F, Omega; // 获取基本角距 GetEarthNutationParameter(dt, &D, &M, &Mp, &F, &Omega); double resulte = 0.0; // 计算章动的周期项 for (int i = 0; i < sizeof(nutation) / sizeof(nutation[0]); i++) { double sita = nutation[i].D * D + nutation[i].M * M + nutation[i].Mp * Mp + nutation[i].F * F + nutation[i].omega * Omega; resulte += (nutation[i].sine1 + nutation[i].sine2 * T) * sin(sita); } // 先乘以章动表的系数 0.0001,然后换算成度的单位 return resulte * 0.0001 / 3600.0;}GetEarthNutationParameter()辅助函数用于计算5个基本角距:
void GetEarthNutationParameter(double dt, double *D, double *M, double *Mp, double *F, double *Omega) { double T = dt * 10; // 从 J2000 起算的儒略世纪数 double T2 = T * T; double T3 = T2 * T; // 平距角(如月对地心的角距离) *D = 297.85036 + 445267.111480 * T - 0.0019142 * T2 + T3 / 189474.0; // 太阳(地球)平近点角 *M = 357.52772 + 35999.050340 * T - 0.0001603 * T2 - T3 / 300000.0; // 月亮平近点角 *Mp = 134.96298 + 477198.867398 * T + 0.0086972 * T2 + T3 / 56250.0; // 月亮纬度参数 *F = 93.27191 + 483202.017538 * T - 0.0036825 * T2 + T3 / 327270.0; // 黄道与月亮平轨道升交点黄经 *Omega = 125.04452 - 1934.136261 * T + 0.0020708 * T2 + T3 / 450000.0;}同样,计算交角章动的实现代码是:
double CalcEarthObliquityNutation(double dt) { double T = dt * 10; // 从 J2000 起算的儒略世纪数 double D, M, Mp, F, Omega; // 获取基本角距 GetEarthNutationParameter(dt, &D, &M, &Mp, &F, &Omega); double resulte = 0.0; // 计算交角章动的周期项 for (int i = 0; i < sizeof(nutation) / sizeof(nutation[0]); i++) { double sita = nutation[i].D * D + nutation[i].M * M + nutation[i].Mp * Mp + nutation[i].F * F + nutation[i].omega * Omega; resulte += (nutation[i].cosine1 + nutation[i].cosine2 * T) * cos(sita); } // 先乘以章动表的系数 0.0001,然后换算成度的单位 return resulte * 0.0001 / 3600.0;}除了章动修正,对于目测系统来说,还要进行光行差修正。光行差是指在同一瞬间,运动中的观察者所观测到的天体视方向与静止的观测者所观测到天体的真方向之差。造成光行差的原因有两个,一个是光的有限速度,另一个是观察者的运动。在地球上的天文观测者因和地球一起运动(自传+公转),他所看到的星光方向与假设地球不动时看到的方向不一样。以太阳为例,光线从太阳传到地球需要约8分钟的时间,在这8分钟多的时间中,地球沿着公转轨道移动了一段距离人们根据现在的观察认定太阳在那个视位置,事实上那是8分钟前太阳的位置。在精确的天文计算中,需要考虑这种光行差引起的视位置差异,在计算太阳的地心视黄经时,要对其进行光行差修正。地球上的观测者可能会遇到几种光行差,分别是因地球公转引起的周年光行差,因地球自传引起的周日光行差,还有因太阳系或银河系运动形成的长期光行差等等,对于从地球上观察太阳这种情况,只需要考虑周年光行差和周日光行差。因太阳公转速度比较快,周年光行差最大可达到20.5角秒,在计算太阳视黄经时需要考虑修正。地球自传速度比较慢,周日光行差最大约为零点几个角秒,因此计算太阳视黄经时忽略周日光行差。
下面是一个粗略计算太阳地心黄经光行差修正量的公式,其中R是地球和太阳的距离:
AC = -20′.4898 / R (3.17式)
分子20.4898并不是一个常数,但是其只的变化非常缓慢,在0年是20′.4893,在4000年是20′.4904。前文提到过,太阳到地球的距离R可以用VSOP87D表的R0-R5周期项计算出来,R的单位是“天文单位(AU)”,和计算太阳地心黄经和地心黄纬类似,太阳到地球的距离可以这样算出来:
double CalcSunEarthRadius(double dt) { // 计算各阶的周期项 double R0 = CalcPeriodicTerm(Earth_R0, sizeof(Earth_R0) / sizeof(VSOP87_COEFFICIENT), dt); double R1 = CalcPeriodicTerm(Earth_R1, sizeof(Earth_R1) / sizeof(VSOP87_COEFFICIENT), dt); double R2 = CalcPeriodicTerm(Earth_R2, sizeof(Earth_R2) / sizeof(VSOP87_COEFFICIENT), dt); double R3 = CalcPeriodicTerm(Earth_R3, sizeof(Earth_R3) / sizeof(VSOP87_COEFFICIENT), dt); double R4 = CalcPeriodicTerm(Earth_R4, sizeof(Earth_R4) / sizeof(VSOP87_COEFFICIENT), dt); // 计算地球半径 double R = (((((R4 * dt) + R3) * dt + R2) * dt + R1) * dt + R0) / 100000000.0; return R;}也可以不使用VSOP,而用下面的公式直接计算日地距离R:
R = 1.000001018 (1 – e2) / (1 e * cos(v)) (3.18式)
其中e是地球轨道的离心率:
e = 0.016708617 – 0.000042037 * T – 0.0000001236 * T2 (3.19式)
v的计算公式是v = M C,其中M是太阳平近地角:
M = 357.52910 35999.05030 * T – 0.0001559 * T2 – 0.00000048 * T3 (3.20式)
中心C的太阳方程:
C = (1.914600 - 0.004817 * T - 0.000014 * T2) * sin(M)+ (0.019993 - 0.000101 * T) * sin(2M)+ 0.000290 * sin(3M) (3.21式)以上各式中的T都是儒略世纪数,M和C的单位都是度,带入3.18式计算时需要转换成弧度单位,计算出R以后,就可以这样计算光行差修正量:
AC = K / R (K是光行差常数,K = 20′.49552) (3.22式)
无论是使用3.17式还是使用3.22式,最终计算出来的太阳光行差修正单位都是角秒。
由VSOP87理论计算出来的几何位置黄经,经过坐标转换,章动修正和光行差修正后,就可以得到比较准确的太阳地心视黄经,GetSunEclipticLongitudeEC()函数就是整个过程的代码:
double GetSunEclipticLongitudeEC(double jde){double dt = (jde - JD2000) / 365250.0; /*儒略千年数*/// 计算太阳的地心黄经double longitude = CalcSunEclipticLongitudeEC(dt);// 计算太阳的地心黄纬double latitude = CalcSunEclipticLatitudeEC(dt) * 3600.0;// 修正精度longitude += AdjustSunEclipticLongitudeEC(dt, longitude, latitude);// 修正天体章动longitude += CalcEarthLongitudeNutation(dt);// 修正光行差/*太阳地心黄经光行差修正项是: -20".4898/R*/longitude -= (20.4898 / CalcSunEarthRadius(dt)) / (20 * PI);return longitude;}
参数jde是力学时时间,单位是儒略日,返回太阳地心视黄经,单位是度。
到现在为止,我们已经知道如何使用VSOP82/87理论计算以儒略日为单位的任意时刻的太阳地心视黄经,但是这和实际历法计算需求还不一致,历法计算需要根据太阳地心视黄经反求出此时的时间。VSOP82/87理论没有提供反向计算的方法,但是可以采用根据时间正向计算太阳视黄经,配合误差修正进行迭代计算的方法,使正向计算出来的结果向已知结果收敛,当达到一定的迭代次数或计算结果与已知结果误差满足精度要求时,停止迭代,此时的正向输入时间就是所求的时间。地球公转轨道是近似椭圆轨道,轨道方程不具备单调性,但是在某个节气附件的一小段时间区间中,轨道方程具有单调性,这个是本文迭代算法的基础。
实际上,我们要做的事情就是求解方程的根,但是我们面临的这个方程没有求根公式。对此类问题,数学上通常采用的迭代求解方法有二分逼近法和牛顿迭代法,事实上二分逼近法可以用更好的策略,比如用黄金分割代替二分法进行逼近区间的选择。接下来我们将分别介绍这两种方法在计算二十四节气中的应用,首先介绍黄金分割逼近法。
已知太阳视黄经的值,反求对应的时间的过程是这样的,首先根据节气对应的视黄经角度值W,估算出节气可能的时间区间[A, B],然后找到这个时间区间内黄金分割点对应的时间值C,C的计算采用3.23式:
C = ((B – A) * 0.618) A (3.23式)
用C值估算出太阳视黄经W’,如果W’ > W,则调整调迭代时间区间为[A, C],如果W’ < W,则调整迭代时间区间为[C, B],然后重复上述过程,直到W’ 与W的差值满足精度要求为止(区间上下限A和B的差值小于门限制也可以作为迭代退出条件)。采用黄金分割法进行逼近求值的算法实现如下:
double CalculateSolarTerms(int year, int angle) { double lJD, rJD; // 估算迭代起始时间区间 EstimateSTtimeScope(year, angle, lJD, rJD); double solarTermsJD = 0.0; double longitude = 0.0; do { // 通过0.618法则取接近黄金分割点的时间 solarTermsJD = ((rJD - lJD) * 0.618) + lJD; // 获取当前儒略日的太阳黄经 longitude = GetSunEclipticLongitudeECDegree(solarTermsJD); /* 对黄经0度迭代逼近时,由于360度圆周性,黄经值可能落在(345, 360]或[0, 15)区间。 如果值落入前一个区间,需要修正为负数以保证连续性。 */ if (angle == 0 && longitude > 345.0) { longitude -= 360.0; } // 根据黄经值调整迭代范围 if (longitude > static_cast<double>(angle)) { rJD = solarTermsJD; } else { lJD = solarTermsJD; } } while ((rJD - lJD) > 0.0000001); // 精度控制,迭代至满足条件 return solarTermsJD;}这里要特别说明一下,由于角度的360度圆周性,当在太阳黄经0度附近逼近时,区间的上下界可能分别位于(345, 360]和[0, 15)两个区间上,此时需要将(345, 360]区间修正为(-15, 0],使得逼近区间边界的选取能够正常进行。EstimateSTtimeScope()函数估算节气的时间区间,估算的依据是每个月的节气时间比较固定,最多相差一两天,考虑的几千年后岁差的影响,这个估算范围还可以再放宽一点,比如,对于月内的第一个节气,可以将时间范围估算为4日到9日,对于月内的第二个节气,可以将时间范围估算为16日到24日,保证迭代范围内有解。EstimateSTtimeScope()函数算法简单,这里就不列出代码了。
二分逼近或黄金分割逼近算法实现简单,很容易控制,但是也存在效率低,收敛速度慢的问题,现在我们介绍牛顿迭代法,牛顿迭代法是一种在实数域和复数域上近似求解方程的方法。假设我们要求解的方程是f(x) = 0,如果f(x)的导函数f’(x)是连续的,则在真实解x附近的区域内任意一点x0开始迭代,则牛顿迭代法必收敛,特别当f’(x)不等于0的时候,牛顿迭代法是平方收敛的,也就是说,每迭代一次,结果的有效数字将增加一倍。
简单的说,对于方程f(x) = 0,f(x)的导函数是f’(x),则牛顿迭代法的迭代公式是:
Xn 1 = xn – f(xn)/f’(xn) (3.24式)
现在问题就是如何确定方程f(x)。对于我们面临的问题,可以理解为已知angle,通过GetSunEclipticLongitudeEC(solarTermsJD)函数反向求解solarTermsJD的值,因此我们的方程可以理解为:
f(x) = GetSunEclipticLongitudeEC(x) – angle = 0
确定了方程f(x),剩下的问题就是求导函数f’(x)。严格的求解,应该根据GetSunEclipticLongitudeEC()函数,以儒略千年数dt为自变量,按照函数求导的规则求出导函数。因为GetSunEclipticLongitudeEC()函数内部是调用其他函数,因此可以理解为是一个多个函数组合的复合函数,类似f(x) = g(x) h(x, k(x)) p(x)这样的形式,可以按照求导规则逐步对其求导得到导函数。但是我不打算这么做,因为我有更简单的方法,那就是使用计算导数的近似公式。其实求导函数的目的就是为了得到某一点的导数,如果有近似公式可以直接得到这一点的导数,就不用费劲求导函数了。
如果函数f(x)是单调函数,或者是在某个区间上是单调函数,则在此函数的其单调区间上某一点的导数值可以用近似公式计算,这个近似公式是:
f’(x0) = (f(x0 0.000005) – f(x0 – 0.000005)) / 0.00001 (3.25式)
这是一个精度很高的近似公式,完全可以满足民用历法计算的精度要求。
根据以上分析结果,使用牛顿迭代法求解节气的算法就很容易实现了,以下就是牛顿迭代法求解节气的代码:
double CalculateSolarTermsNewton(int year, int angle) { double JD0, JD1, stDegree, stDegreep; // 获取节气的初始儒略日估计值 JD1 = GetInitialEstimateSolarTerms(year, angle); do { // 保存当前迭代值 JD0 = JD1; // 计算当前黄经差值(太阳黄经 - 节气目标黄经) stDegree = GetSunEclipticLongitudeECDegree(JD0) - angle; // 计算黄经对时间的导数(数值微分) stDegreep = (GetSunEclipticLongitudeECDegree(JD0 + 0.000005) - GetSunEclipticLongitudeECDegree(JD0 - 0.000005)) / 0.00001; // 牛顿迭代更新公式 JD1 = JD0 - stDegree / stDegreep; } while (fabs(JD1 - JD0) > 0.0000001); // 精度控制,直到满足条件 return JD1;}经过验证,牛顿迭代法具有非常好的收敛效果,一般只需3次迭代就可以得到满足精度的结果。
至此,我们就有了完整的计算节气发生时间的方法,输入年份和节气对应的太阳黄经度数,即可求的节气发生的精确时间。最后说明一下,以上算法中讨论的时间都是力学时时间(TD),与国际协调时(UTC)以及各个时区的本地时间都有不同,以上计算出来的时间都需要调整成本地时间,比如中国的中原地区就是东八区标准时(UTC 8)。关于力学时、国际协调时(世界时)的定义,请参考文末的小知识3:力学时、原子时和国际协调时。应用本文的算法计算出2012年各个节气的时间如下(已经转换为东八区标准时),与紫金山天文台发布的《2012中国天文年历》中发布的时间在分钟级别上完全吻合(此年历只精确到分钟):
2012-01-06, 06:43:54.28 小寒
2012-01-21, 00:09:49.08 大寒
2012-02-04, 18:22:22.53 立春
2012-02-19, 14:17:35.37 雨水
2012-03-05, 12:21:01.56 惊蛰
2012-03-20, 13:14:24.17 春分
2012-04-04, 17:05:34.65 清明
2012-04-20, 00:12:03.28 谷雨
2012-05-05, 10:19:39.54 立夏
2012-05-20, 23:15:30.28 小满
2012-06-05, 14:25:52.96 芒种
2012-06-21, 07:08:46.98 夏至
2012-07-07, 00:40:42.66 小暑
2012-07-22, 18:00:50.72 大暑
2012-08-07, 10:30:31.88 立秋
2012-08-23, 01:06:48.41 处暑
2012-09-07, 13:28:59.41 白露
2012-09-22, 22:48:57.14 秋分
2012-10-08, 05:11:41.45 寒露
2012-10-23, 08:13:32.83 霜降
2012-11-07, 08:25:56.47 立冬
2012-11-22, 05:50:08.09 小雪
2012-12-07, 01:18:55.23 大雪
2012-12-21, 19:11:35.61 冬至
小知识3:力学时、原子时和国际协调时
力学时全称是“牛顿力学时”,也被称作是“历书时”。它描述天体运动的动力学方程中作为时间自变量所体现的时间,或天体历表中应用的时间,是由天体力学的定律确定的均匀时间。力学时的初始历元取为1900年初附近,太阳几何平黄经为279°41′48″.04的瞬间,秒长定义为1900.0年回归年长度的1/31556925.9747。1958年国际天文学联合会决议决定:自1960年开始用力学时代替世界时作为基本的时间计量系统,规定天文年历中太阳系天体的位置都按力学时推算。力学时与世界时之差由观测太阳系天体(主要是月球)定出,因此力学时的测定精度较低,1967年起被原子时代替作为基本时间计量系统。
国际协调时又称世界时,是以本初子午线的平子夜起算的平太阳时,又称格林威治时间。世界各地地方时与世界时之差等于该地的地理经度。世界时1960年以前曾作为基本时间计量系统被广泛应用。由于地球自转速度变化的影响,它不是一种均匀的时间系统。后来世界时先后被历书时和原子时所取代。
原子时是以物质的原子内部发射的电磁振荡频率为基准的时间计量系统。原子时的初始历元规定为1958年1月1日世界时0时,秒长定义为铯-133原子基态的两个超精细能级间在零磁场下跃迁辐射9192631770周所持续的时间。这是一种均匀的时间计量系统。1967年起,原子时已取代力学时作为基本时间计量系统。
参考文章:
[1] 《Secular variations of the planetary orbits》http://www.worldlingo.com/ma/enwiki/en/Secular_variations_of_the_planetary_orbits
[2] Jean.Meeus.Astronomical.Algorithms(天文算法)
[3] M.Chapront-Touze and J.Chapront.ELP 2000-85 – A semi-analytical lunar ephemeris adequate for historical times.Astronomy And Astrophysics,1998
[4] P.Bretagnon and G.Francou.Planetray theories in rectangular and spherical variables VSOP87 solutions. Astronomy And Astrophysics,1998
本站作者简介:万里鸿鹄(wanlihonghu.com),80后,山西太原人。自大学毕业后,先后师从几位民间易学老师,对中华传统易经典籍有一定的研究,热爱易学命理,对于四柱八字、六爻占卜、开店、婚嫁择吉、起名、阳宅风水等有一定学术研究,欢迎朋友们咨询交流。

声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。